이산수학에서 그래프(Graph)는 정점(Vertex)와 간선(Edge)로 이루어진 집합이다.
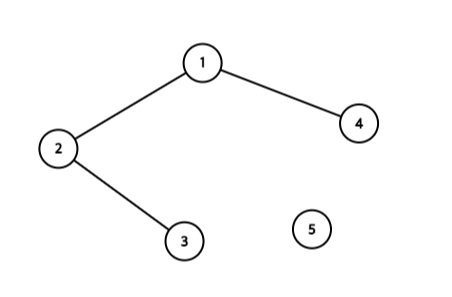
기본적으로 위와 같은 형태이며, 간선은 정점 사이를 연결하는 역할을 한다. 또한 정점은 노드(Node)라고도 부른다. 두 정점 $u,v$가 있을 때, $u$에서 $v$로 가는 간선이 있으면 $u$는 $v$와 연결되어 있다고 한다.
어떤 정점에서 시작해서 다시 자기 자신에게 돌아오는 경로가 있다면 그 경로를 사이클(Cycle)이라고 한다.
일반적으로 정점의 개수를 $\vert V \vert$ 혹은 $V$로 나타내고, 간선의 개수는 $\vert E \vert$ 혹은 $E$로 나타낸다.
간선
간선은 정점과 정점을 연결하는 역할이다. 다음과 같은 특성을 추가로 가질 수 있다.
- 방향(Direction): 특정 방향으로만 연결된 간선이 존재할 수 있다. 보통 화살표로, 무방향 간선은 선분으로 나타낸다.
- 가중치(Weighted value): 가중치는 간선이 가지는 특정 값. 여러 가지 의미가 될 수 있다.
- 용량(Capacity): 용량은 네트워크 유량에서 나타나는 개념이다.
그래프에서 어떤 간선의 시작점과 끝점이 동일한 경우 그 간선을 고리(Loop)라고 한다.
그래프의 종류
그래프는 고유한 특성에 따라 여러 가지로 나눌 수 있다.
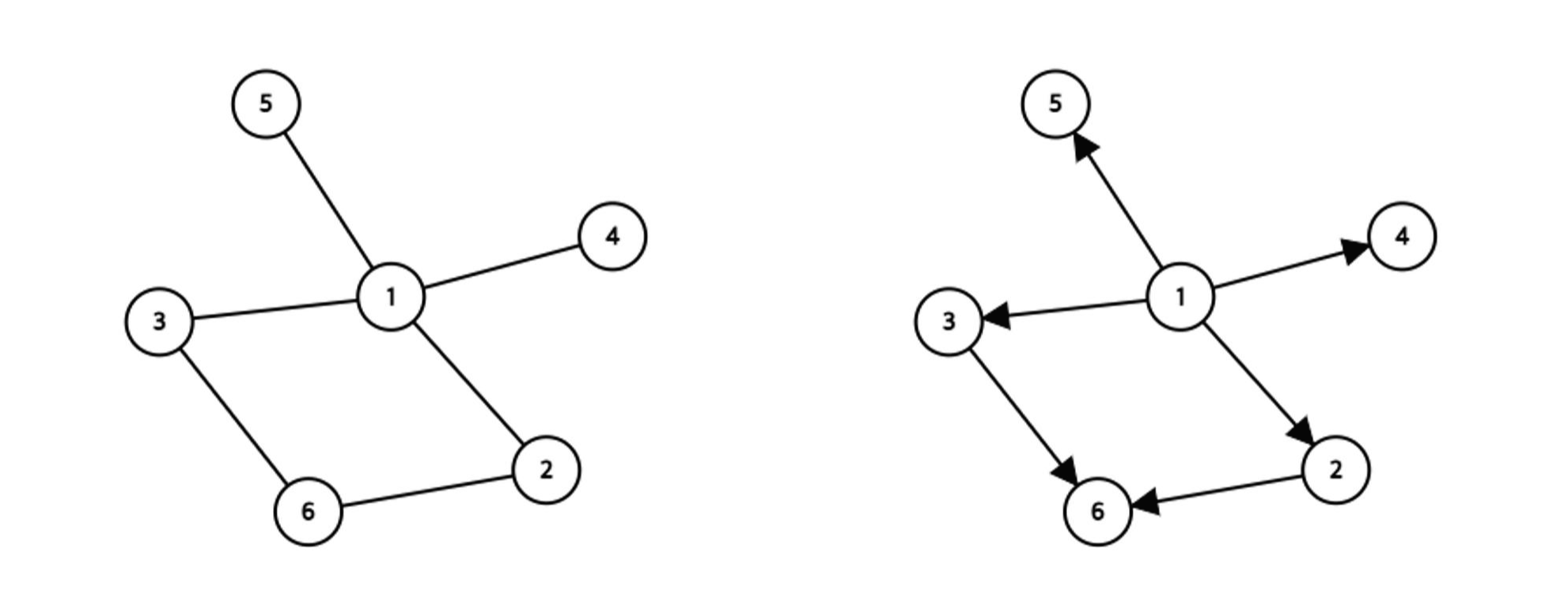
- 간선에 방향이 존재하는 그래프를 유향 그래프(Directed Graph), 방향이 존재하지 않는 그래프를 무향 그래프(Undirected Graph)라고 한다.
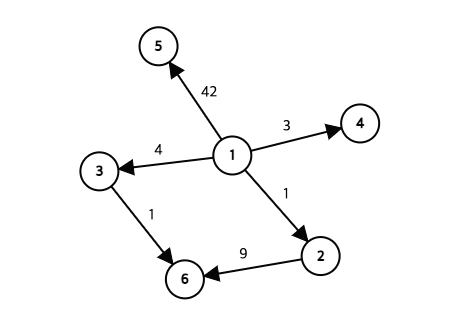
- 간선에 가중치가 존재하는 그래프를 가중치 그래프(Weighted Graph)라고 한다.
- 그래프에서 모든 정점이 서로 연결되어 있는 그래프를 연결 그래프(Connected Graph)라고 한다.
- 부분 그래프(Subgraph)는 어떤 그래프에 속한 일부 정점과 간선들로 이루어진 그래프를 말한다.
- 어떤 정점과 그 정점에 연결된 모든 정점, 간선으로 이루어진 부분 그래프를 컴포넌트(Component)라고 한다.
- 무향 그래프에서 서로 다른 두 정점을 연결하는 간선이 항상 존재하는 그래프를 완전 그래프(Complete Graph)라고 한다.
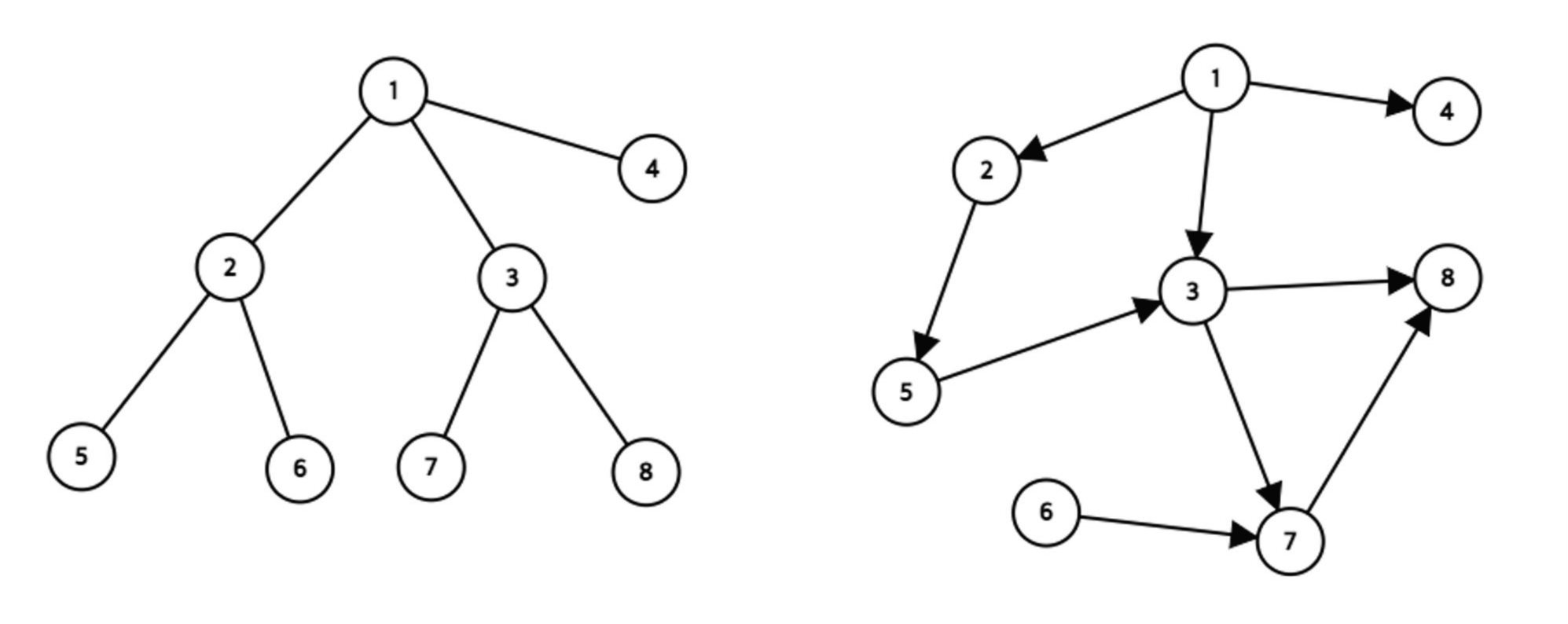
- 사이클이 없는 무향 그래프를 트리(Tree), 유향 그래프를 DAG(Directed Acyclic Graph)라고 한다.
그래프의 표현

위 그래프는 1번 정점은 2, 4번 정점과 연결되어 있고 2번 정점은 3, 4번 정점, 3번 정점은 4번 정점과 연결되어 있다.
인접 행렬(Adjacency matrix)은 $V \times V$ 크기의 행렬로, 어떤 정점이 다른 정점과 연결되어 있는지 여부와 가중치를 나타낸다. 위 그래프를 인접 행렬로 나타내면 다음과 같다.
0 1 0 1
0 0 1 1
0 0 0 1
0 0 0 0주로 2차원 배열로 나타내며, 정점 $u,v$가 연결되어 있는지 확인하기 위해서는 adj[u][v]를 확인하면 된다. ($O(1)$ 시간이 소요) 공간 복잡도는 $O(V^2)$이다. 구현과 간선의 삽입은 다음처럼 할 수 있다.
int adj[MAX][MAX]; // 인접 행렬
adj[a][b] = adj[b][a] = 1; // a <-> b 간선 삽입
인접 리스트(Adjacency list)는 연결 리스트 혹은 동적 배열을 이용하여 정점별로 연결된 다른 정점을 나타낸 것이다. 위에서 인접 행렬로 나타낸 그래프를 인접 리스트로 표현하면 다음과 같다.
1: [2, 4]
2: [3, 4]
3: [4]
4: []정점 $u,v$가 연결되어 있는지 확인하기 위해서는 $u$에 해당하는 리스트를 순회해야 하며, 최대 $O(V)$ 시간이 소요된다. 공간 복잡도는 $O(V+E)$이다. 구현은 다음과 같다.
vector<int> adj[MAX]; // 인접 리스트
adj[a].push_back(b);
adj[b].push_back(a); // a <-> b 간선 삽입