유니온 파인드(Union-Find), 또는 분리 집합(서로소 집합, Disjoint Set)은 여러 집합들을 표현하는 자료 구조다. Disjoint Set이라는 이름에서도 알 수 있듯이, 이 자료 구조가 표현하는 집합은 서로소이고, 모든 집합의 합집합은 전체집합이다.
Union-Find라는 이름은 이 자료 구조가 기본적으로 두 가지 연산, 즉 union과 find만을 지원하기에 붙여진 이름이다. union 연산은 두 집합을 하나로 합치는 연산이고, find 연산은 어떤 원소가 어느 집합에 속하는지 알아내는 연산이다.
초기 상태의 유니온 파인드는 1~N까지의 원소(이건 0-index일 수도 있음)가 전부 크기 1인 집합에 담겨 있다. 여기에서 어떤 두 집합에 union 연산을 수행하면 두 집합이 하나로 합쳐진다. 초기화는 다음과 같이 할 수 있다.
int par[MAX];
void init(int n) { // 크기가 n이 되게 초기화
for (int i = 1; i <= n; i++) par[i] = i;
}배열을 이용한 유니온 파인드
위의 설명을 배열을 이용하여 구현하는 것은 어렵지 않다. par[i] = $i$가 속하는 집합의 번호라고 정의하면 find 연산은 다음과 같이 구현할 수 있다. 시간 복잡도는 $O(1)$이다.
int find(int v) {
return par[v];
}
union 연산은 집합 $A, B$를 합칠 때, 1부터 N까지 순회하면서 집합 $B$에 속하는 원소를 $A$에 속한다고 바꿔주면 된다. 시간 복잡도는 $O(n)$이다. 함수 이름이 merge인 이유는 union은 예약어이기 때문이다.
void merge(int a, int b) {
a = find(a), b = find(b);
if (a == b) return;
for (int i = 1; i <= n; i++) {
if (par[i] == b) par[i] = a;
}
}
이렇게 구현하면 union 연산이 너무 느리다. 더 좋은 방법은 없을까?
트리를 이용한 유니온 파인드
집합을 트리로 표현하는 방법이 있다. 트리에는 루트가 존재하기 때문에, 이제 집합의 번호를 루트의 번호로 정의할 수 있다.
find 연산은 특정 노드에서 계속 부모 노드를 따라 올라가다 보면 루트를 만나게 되고, 그 루트가 "찾으려고 하는 노드가 속한 집합의 번호"이다. 수행 시간은 트리의 깊이에 비례하게 된다.
int find(int v) {
if (par[v] == v) return v;
return find(par[v]);
}
union 연산은 $B$를 $A$가 속한 트리의 자손으로 넣어서 해결할 수 있다. 역시 수행 시간이 트리의 깊이에 비례한다.
void merge(int a, int b) {
a = find(a), b = find(b);
if (a == b) return;
par[v] = u;
}
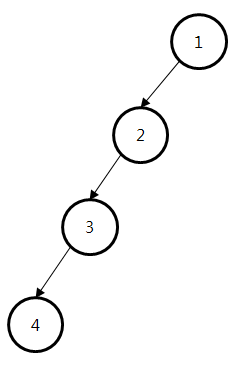
그런데 이런 방식으로 구현하면 위의 그림 같은 트리가 만들어질 수 있다. 이럴 경우에는 트리의 높이가 최대 $O(n)$이기 때문에, find와 union 연산 모두 $O(n)$이 되어 버린다. 오히려 배열보다 성능이 떨어지게 된다.
유니온 파인드의 최적화
다행히도 몇 가지 최적화를 수행하면 매우 큰 속도 향상을 가져올 수 있다.
우선 두 트리를 합칠 때 높이가 높은 트리를 넣는 것보다 더 낮은 트리를 높은 트리 밑에 넣어주는 것이 더 효율적이다. rank[i] = i번 노드를 루트로 하는 서브트리의 높이 근사값이라고 하면 union 연산을 다음처럼 구현할 수 있다. 이러한 최적화를 Union by Rank라고 한다.
int par[MAX], rank[MAX];
void init(int n) {
for (int i = 1; i <= n; i++) par[i] = i, rank[i] = 1;
}
// find 생략
void merge(int a, int b) {
a = find(a), b = find(b);
if (a == b) return;
if (rank[a] > rank[b]) swap(a, b);
par[a] = b;
if (rank[a] == rank[b]) rank[b]++;
}
또한 find 연산을 했을 때 다음 번에 결과가 바뀌는 일은 없다. 그렇기 때문에 재귀 함수로 호출하는 동안 거쳐간 모든 노드를 바로 루트의 자식이 되게 옮겨주면 다음 번에 find 연산을 수행할 때 연산량이 매우 많이 줄어든다. 이러한 최적화를 경로 압축이라고 하며 다음과 같이 구현할 수 있다.
int find(int v) {
if (par[v] == v) return v;
return par[v] = find(par[v]);
}
이렇게 두 가지 최적화를 적용한 유니온 파인드의 시간 복잡도는 평균적으로 $O(\alpha(n))$이라고 한다. $\alpha(n)$은 아커만 함수의 역함수로 매우 느리게 증가해 가능한 모든 $n$에 대해 $5$ 미만이므로 사실상 상수 시간 복잡도라고 볼 수 있다.
Weighted Union-Find
위처럼 구현하면 rank 배열을 가지고 있어야 하므로 메모리 사용량이 두 배가 된다. 이를 해결하기 위해 고안된 방법이 Weighted Union-Find이다.
우선 par[i]는 i가 트리의 루트이면(i == find(i)이면) $-1 \times$(집합의 크기)다. i가 트리의 루트가 아니면 원래대로 i의 부모인 노드의 번호를 저장하고 있다. 따라서 루트인지 판별하려면 par[i] < 0을 확인하면 된다.
union 연산에서 집합을 합칠 때는 큰 쪽에 작은 쪽의 크기를 더해주고 똑같은 방법으로 합치면 된다. 그리고 이제 루트는 집합의 크기를 가지고 있기 때문에, 원소 $n$이 포함된 집합의 크기를 알 수 있다. 바로 -par[find(n)]다.
최종적인 유니온 파인드의 구현은 다음과 같다.
struct UnionFind {
vector<int> par;
void init(int sz) {
par.resize(sz + 1);
fill(par.begin(), par.end(), -1);
}
int find(int v) {
if (par[v] < 0) return v;
return par[v] = find(par[v]);
}
void merge(int a, int b) {
a = find(a), b = find(b);
if (a == b) return;
if (par[a] > par[b]) swap(a, b);
par[a] += par[b];
par[b] = a;
}
int size(int v) {
return -par[find(v)];
}
};